순수 굽힘 (2) - 굽힘 모멘트를 받을때 변형과 변형률 본문
이번에는 대칭평면을 지나며 크기가 같고 방향이 반대인 모멘트가 작용하는 균일단면 부재에 대해 생각해보겠습니다.
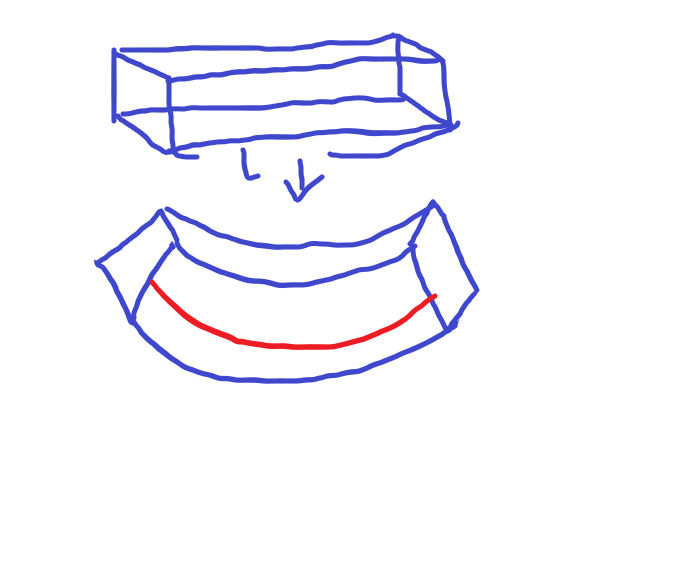
이러한 단면 부재가 모멘트를 받아 구부러지면, 중간의 중립면 (그림에서는 빨간 부분) 을 제외하고는 그 길이가 L에서 변화하게 될 것입니다.
양의 방향 모멘트일 경우에, 중립면 기준 윗부분은 압축, 밑부분은 인장력을 받게 될 것입니다.

이때 구부러진 부재를 보겠습니다. 부재가 구부러진 방향으로 연장선을 그어 만나는 부분의 각도를 Θ 라고 하고
만나는 부분까지의 길이를 \(\rho\) 라고 하겠습니다.
그렇다면, 호의 길이 공식으로 \(\rho\)Θ = L 이 됩니다.
이때 부재위의 임의의 면 (중립면과 평행) 까지의 거리를 y라고 하고
이 임의의 면의 길이를 L'이라고 한다면,
변형률 \(\epsilon_x\) = \(\frac{L'-L}{L}\) = \(\frac{(\rho - y)Θ-\rhoΘ}{\rhoΘ}\) = \(\frac{-y}{\rho}\)
이때 최대의 변형률을 \(\epsilon_{M}\) (변형률의 최대 절댓값) 라고 하면
\(\epsilon_M\) = \(\frac{c}{\rho}\)
\(\epsilon_M\) 은 l \(\epsilon_M\) l 한 값입니다.
이제 일반 변형률과 최대 변형률의 관계를 식으로 나타내면,
\(\epsilon_x\) = \(\frac{-y}{c}\)*\(\epsilon_M\)이 됩니다.
'재료역학' 카테고리의 다른 글
| 순수굽힘 (3) - 탄성영역 내에서의 굽힘 / 탄성휨공식,휨응력,휨저항,휨성 ,단면계수 (0) | 2019.05.22 |
|---|---|
| 순수 굽힘 (1) - 굽힘모멘트 / 굽힘모멘트 부호 (0) | 2019.05.22 |
| 평행축 정리 - 단면 2차 모멘트 변화 / 극관성모멘트의 변화 (0) | 2019.05.22 |
| 단면 2차 모멘트와 극관성 모멘트, 극관성모멘트 유도 (0) | 2019.05.22 |
| 단면 1차 모멘트의 모든것 - 도심 , 합성단면 등 (0) | 2019.05.21 |



