단면 1차 모멘트의 모든것 - 도심 , 합성단면 등 본문

위의 그림에서 생각해 보겠습니다.
우선 단면 1차 모멘트라 하면 의미는 따로 없습니다. 이것으로 도심이나 극관성모멘트 등을 구할 수 있는
하나의 도구라고 생각하시면 편할 것 같습니다.
단면 1차모멘트는 축에 대하여 정의되는데,
위의 그림에서 x축에 관한 단면 1차 모멘트 \(Q_x\) = ∫ydA 인데, 이것은 미소 단면적에서 x축까지의
수직거리와 미소 단면적을 곱해준 값이 됩니다.
마찬가지로 y축에 관한 단면 1차 모멘트 \(Q_y\) = ∫xdA 가 됩니다.
단면 1차 모멘트의 단위는 \(m^3\) 혹은 \(mm^3\)을 사용합니다.
이러한 단면 1차 모멘트로 단면적의 도심을 구할 수 있는데 바로
\(Q_x\) = ∫ydA = A\(\overline{y}\) 이 됩니다.
물론 \(Q_y\) = ∫xdA = A\(\overline{x}\) 도 성립합니다.
따라서 \(\overline{x}\) = \(\frac{∫xdA}{A}\) 인데
구분구적분으로 \(\overline{x}\) = \(\frac{\sum x_iA_i}{A}\) 으로 표현하기도 합니다.
도심은 만약 단면이 대칭축을 가지고 있다면 그 대칭축 상에 위치하게 됩니다.
그리고 그 대칭축에 대한 모멘트값은 0이 됩니다.
또한 단면이 대칭중심점 O를 가지고 있을 경우 그 점을 통과하는 축에 대한 모멘트값은 0이 됩니다.

그림으로 보면 위의 그림에서 O를 기준으로 대칭을 이루고 있습니다. 여기서 O를 통과하는 축에 대한
모멘트 값은 0이 됩니다.
그렇다면 단면 1차 모멘트를 통해 도심을 구하는 법을 생각해 보겠습니다.
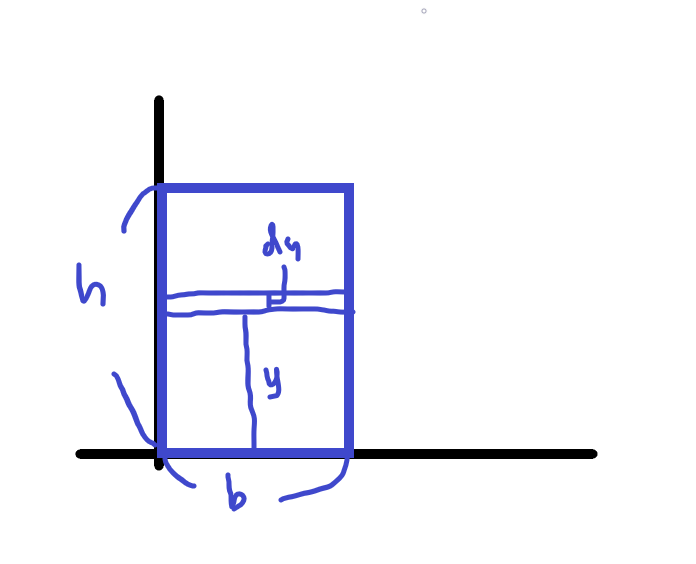
위의 그림에서 직사각형을 생각해보면 x축에 대한 단면 1차 모멘트 값은
∫ydA인데 여기서 dA = b*dy가 되되므로
∫ydA= \(\int_{0}^{h}\)ybdy 가 됩니다.
따라서 그 값은 \(\frac{bh^2}{2}\) 가 되고
이것은 A\(\overline{y}\)가 됩니다.
따라서 \(\overline{y}\) = \(\frac{bh^2}{2A}\) = \(\frac{h}{2}\) 가 됩니다.
물론 도심의 y좌표는 직관적으로 \(\frac{h}{2}\) 임을 알 수 있습니다.
x축에서도 방법은 동일합니다.
이것을 삼각형에서도 해보겠습니다.
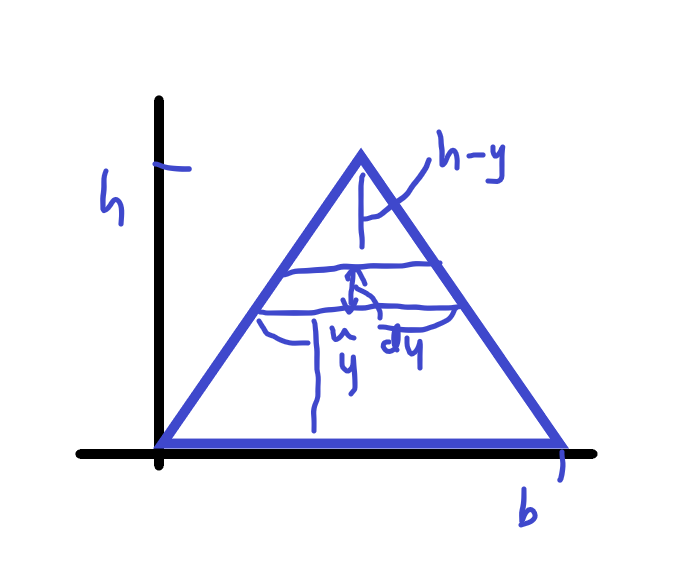
그림에서 미소 단면의 높이가 dy이고 밑변이 u일때
b : h = u : h-y 가 성립합니다.
따라서 u=\(frac{b(h-y)}{h}\) 이고 dA=udy입니다.
\(Q_x\) = \(\int_{0}^{h}\)yudy = \(frac{b}{h}\)\(\int_{0}^{h}\)y(h-y)dy = \(frac{bh^2}{6}\)
이 됩니다.
복잡한 단면일 경우
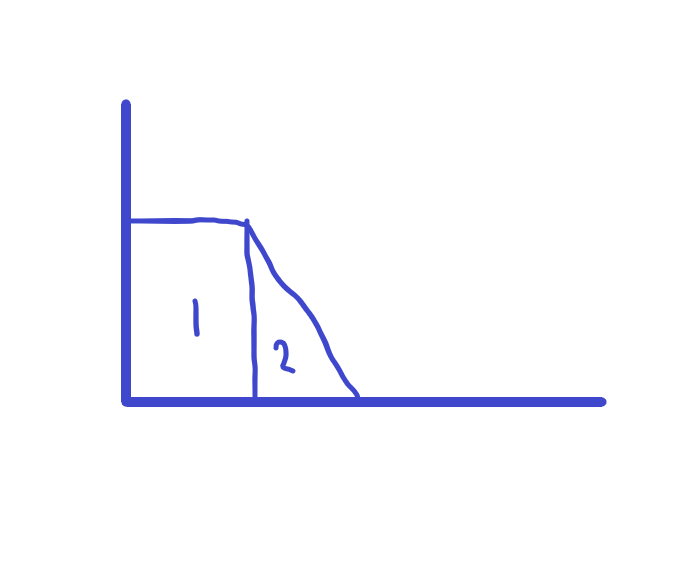
위의 그림과 같이 나누어서 계산하면 됩니다.
\(\overline{x}\) = \(\frac{\sum x_iA_i}{A}\) 이므로 그 값을 더해주면 도심의 좌표를 구할 수 있습니다.
'재료역학' 카테고리의 다른 글
| 평행축 정리 - 단면 2차 모멘트 변화 / 극관성모멘트의 변화 (0) | 2019.05.22 |
|---|---|
| 단면 2차 모멘트와 극관성 모멘트, 극관성모멘트 유도 (0) | 2019.05.22 |
| 비틀림 (5) - 비 원형 부재의 비틀림 - 균일 직사각형 단면 / 얇은 비원형 중공축 / 전단 흐름 (0) | 2019.05.19 |
| 비틀림 (4) - 전동축의 설계 /동력,각속도 (0) | 2019.05.19 |
| 비틀림 (3) - 탄성 한계 내에서 비틀림각 (균일 단면, 불균일 단면) (0) | 2019.05.19 |


