순수굽힘 (3) - 탄성영역 내에서의 굽힘 / 탄성휨공식,휨응력,휨저항,휨성 ,단면계수 본문

https://new-material.tistory.com/68
순수 굽힘 (1) - 굽힘모멘트 / 굽힘모멘트 부호
우선 순수 굽힘이라는 것의 뜻을 말하자면, 그림과 같이 시편의 길이 방향의 면에 크기가 같고 방향이 반대인 우력이 작용하는 것을 의미합니다. 이때 모멘트 M과 M'은 이러한 시편을 구부리려고 하는데, 이때의..
new-material.tistory.com
https://new-material.tistory.com/69
순수 굽힘 (2) - 굽힘 모멘트를 받을때 변형과 변형률
이번에는 대칭평면을 지나며 크기가 같고 방향이 반대인 모멘트가 작용하는 균일단면 부재에 대해 생각해보겠습니다. 이러한 단면 부재가 모멘트를 받아 구부러지면, 중간의 중립면 (그림에서는 빨간 부분) 을 제..
new-material.tistory.com
순수 굽힘 (1)과 (2) 에서 굽힘에 대한 개념과 굽힘 하중을 받았을때 물체의 길이 변형률에 대한 식을 알아 보았습니다.
역학에서는 이러한 식이 탄성영역에서 어떻게 거동되는지 알아보는 것이 굉장히 중요하므로,
이번 포스팅에서는 탄성영역에서의 굽힘에 대해 알아보도록 하겠습니다.
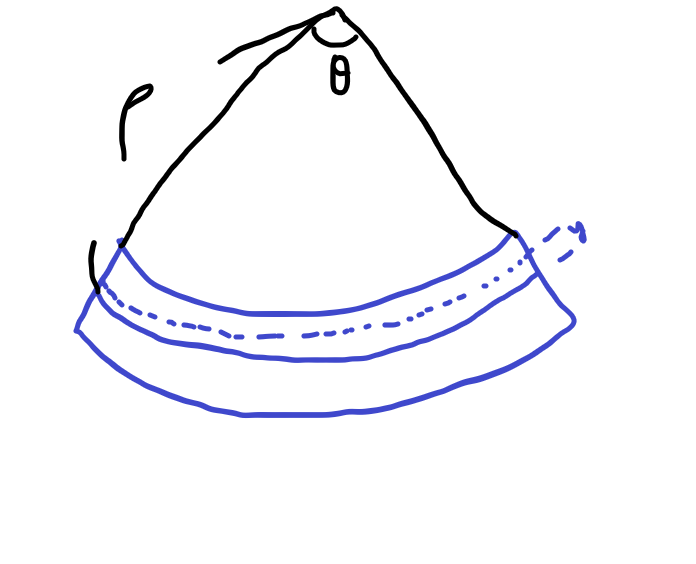
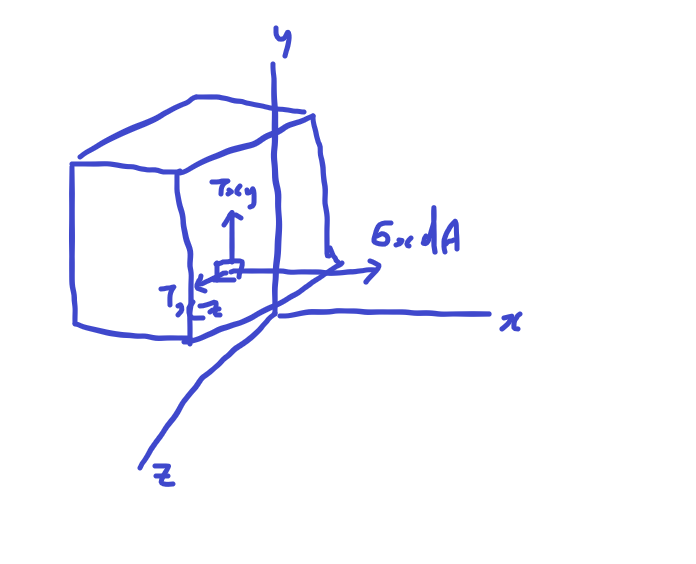
탄성영역에서 변형률은 훅의 법칙이 적용 가능합니다.
따라서 \(\sigma_x\) = E*\(\epsilon_x\) 이 되고
\(\epsilon_x\) = \(\frac{-y}{c}\)\(\epsilon_M\)이므로
\(\sigma_x\) = \(\frac{-y}{c}\)E\(\epsilon_M\)이 됩니다.
따라서 \(\sigma_x\) = \(\frac{-y}{c}\)\(\sigma_M\) 이라는 식을 얻을 수 있습니다.
이때 \(F_x\) = ∫\(\sigma_x\)dA = ∫\(\frac{-y}{c}\)\(\sigma_M\)dA = 0 이 됩니다.
따라서 여기서 \(\frac{-\sigma_M}{c}\) 는 상수이므로 ∫ydA = 0이 됩니다.
∫ydA는 단면1차모멘트 값이므로 https://new-material.tistory.com/64
단면 1차 모멘트의 모든것 - 도심 , 합성단면 등
위의 그림에서 생각해 보겠습니다. 우선 단면 1차 모멘트라 하면 의미는 따로 없습니다. 이것으로 도심이나 극관성모멘트 등을 구할 수 있는 하나의 도구라고 생각하시면 편할 것 같습니다. 단면 1차모멘트는 축..
new-material.tistory.com
여기서 중립축에 있는 단면의 1차 모멘트가 0이 된다는 걸 알 수 있습니다.
이 뜻은 중립축이 단면에서 도심을 지나는 축이라는 것을 의미합니다.
또한 위의 그림에서 z축에 대해 \(M_z\) = ∫-y\(\sigma_x\)dA 이므로
∫-y\(\sigma_x\)dA = ∫-y\(\frac{-y}{c}\)\(\sigma_M\)dA 이 됩니다.
따라서 식을 정리해보면 \(\frac{\sigma_M}{c}\)∫\(y^2\)dA 이 되는데,
∫\(y^2\)dA는 단면 2차 모멘트 입니다. https://new-material.tistory.com/65
단면 2차 모멘트와 극관성 모멘트, 극관성모멘트 유도
1차 모멘트에 이어 단면 2차 모멘트도 다뤄보도록 하겠습니다. \(I_x\) = ∫\(y^2\)dA로 정의 되는 단면 2차 모멘트는 수직거리의 제곱에 미소단면적을 곱해 적분해 준 값입니다. 이때 미소단면까지의 거리가..
new-material.tistory.com
따라서 M = \(\frac{\sigma_M}{c}\)I 입니다.
이 식을 바꿔쓰면, \(\sigma_M\) = \(\frac{Mc}{I}\) 라는 결론을 얻을 수 있습니다.
여기서 \(\frac{I}{c}\) = S 이며 S는 단면 계수라고 합니다.
\(\sigma_M\) = \(\frac{M}{S}\)
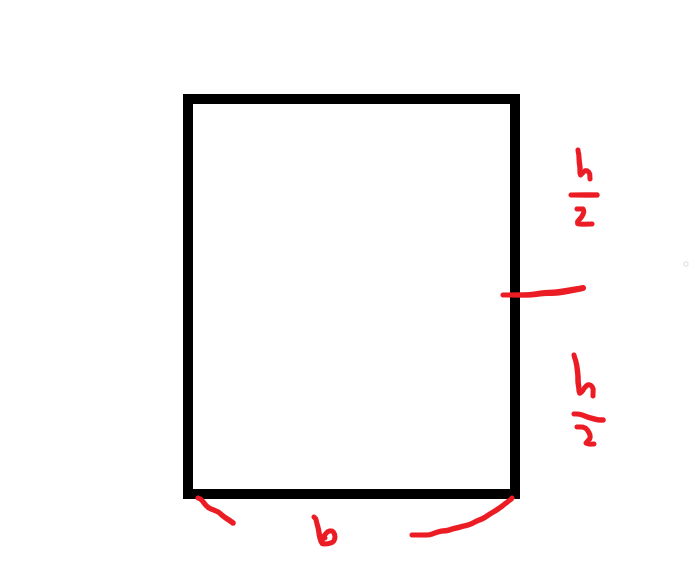
이를 예를들어 높이가 h이고 폭이 b 중립축에서 끝점까지의 거리가 c인 직사각형에 적용하면,
도심에서 단면 2차 모멘트를 구하여
S = \(\frac{I}{c}\) = \(\frac{bh^3}{12}\)*\(\frac{2}{h}\) = \(\frac{bh^2}{6}\) = \(\frac{Ah}{6}\)
임을 알 수 있는데, 단면적 A각 같을때 h가 클 수록 S가 크다는 걸 알 수 있고, S가 커짐에 따라
\(\sigma_M\) = \(\frac{M}{S}\) 이므로 같은 모멘트에 응력값이 작아진다는 것을 알 수 있습니다.
이는 응력값이 작다는 것은 굽힘 저항이 크다는 것을 의미합니다.
따라서 \(\sigma_x\) = \(\frac{My}{I}\) 또한 성립합니다.
이 식을 탄성 휨 공식이라고 합니다.

'재료역학' 카테고리의 다른 글
| 순수 굽힘 (2) - 굽힘 모멘트를 받을때 변형과 변형률 (0) | 2019.05.22 |
|---|---|
| 순수 굽힘 (1) - 굽힘모멘트 / 굽힘모멘트 부호 (0) | 2019.05.22 |
| 평행축 정리 - 단면 2차 모멘트 변화 / 극관성모멘트의 변화 (0) | 2019.05.22 |
| 단면 2차 모멘트와 극관성 모멘트, 극관성모멘트 유도 (0) | 2019.05.22 |
| 단면 1차 모멘트의 모든것 - 도심 , 합성단면 등 (0) | 2019.05.21 |



