비틀림 (3) - 탄성 한계 내에서 비틀림각 (균일 단면, 불균일 단면) 본문
\(\gamma_{max}\)=\(\frac{c\phi}{L}\), \(\tau_{max}\)=\(\frac{Tc}{J}\) 임을 알아 보았다.
이때 G\(\gamma_{max}\)=\(\tau_{max}\)
\(\gamma_{max}\)=\(\frac{\tau}{G}\)=\(\frac{Tc}{JG}\) 이다.
따라서 ∅=\(\frac{Tc}{JG}\)*\(\frac{L}{c}\)=\(\frac{TL}{JG}\) 이다.
이것은 비틀림각 ∅가 물체에 작용하는 토크 T와 비례함을 알려준다.
이때 유도된 식은 균일 단면에 토크가 작용할 경우에 성립한다.
그렇다면 축이 다음과 같이 생긴경우라면 어떨까
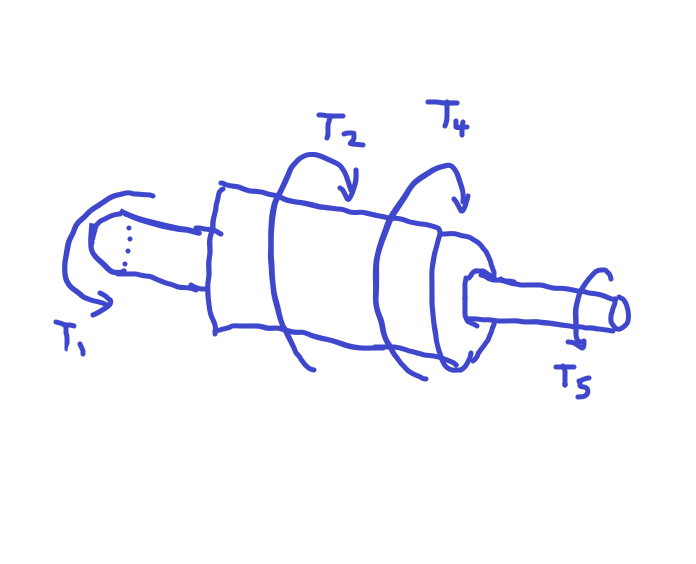
이 경우 축의 단면이 균일하지도 않고 토크가 축단면에만 작용하지도 않고 여러개의 토크가 작용한다.
이때 우선 식으로 표현하자면
∅=∑\(\frac{T_iL_i}{J_iG_i}\)로 알아 보았던 식을 각각 더해준 꼴이 된다.
이번에는 축의 단면이 계속해서 변하는 경우를 생각해보자.
이 경우에는 무한소로 나누어 적분을 통해 더해주어야 한다.

물론 간단하다. L을 무한소로 나누어 각각의 요소를 dx라 하자.
그렇다면 x에 대해 0에서 L까지 적분해 주면 되는 것이다.
'재료역학' 카테고리의 다른 글
| 단면 1차 모멘트의 모든것 - 도심 , 합성단면 등 (0) | 2019.05.21 |
|---|---|
| 비틀림 (5) - 비 원형 부재의 비틀림 - 균일 직사각형 단면 / 얇은 비원형 중공축 / 전단 흐름 (0) | 2019.05.19 |
| 비틀림 (4) - 전동축의 설계 /동력,각속도 (0) | 2019.05.19 |
| 비틀림 (2) - 축과 각도를 이루는 경우 응력 (0) | 2019.05.13 |
| 비틀림 (1) - 우력/비틀림힘/토크/비틀림축/탄성영역에서의 응력/탄성비틀림/극관성모멘트 (0) | 2019.05.13 |


