비틀림 (2) - 축과 각도를 이루는 경우 응력 본문
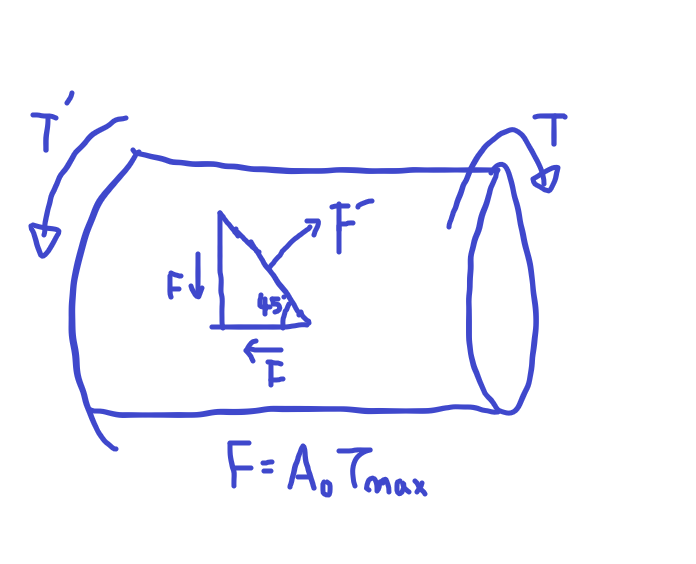
원형축에 토크 T가 작용하여 비틀림을 받고 있다고 하겠습니다.
이때 축 중심선과 45도를 이루고 있는 요소을 살펴보면, 위 그림과 같이 두면에 최대의 전단력이 작용하며 그 힘의 크기는 F=\(A_0\)\(\tau_{max}\)τ(최대) 이고
F'은 인장력으로 그 크기는 2Fcos45로 발생하게 됩니다.
따라서 F'=2\(A_0\)\(\tau_{max}\)cos45=√2\(A_0\)\(\tau_{max}\) 입니다.
그리고 이에 대응하는 응력은
σ=\(\frac{F'}{A}\) = √2\(A_0\)\(\tau_{max}\)/√2\(A_0\)=\(\tau_{max}\) 입니다.
'재료역학' 카테고리의 다른 글
| 단면 1차 모멘트의 모든것 - 도심 , 합성단면 등 (0) | 2019.05.21 |
|---|---|
| 비틀림 (5) - 비 원형 부재의 비틀림 - 균일 직사각형 단면 / 얇은 비원형 중공축 / 전단 흐름 (0) | 2019.05.19 |
| 비틀림 (4) - 전동축의 설계 /동력,각속도 (0) | 2019.05.19 |
| 비틀림 (3) - 탄성 한계 내에서 비틀림각 (균일 단면, 불균일 단면) (0) | 2019.05.19 |
| 비틀림 (1) - 우력/비틀림힘/토크/비틀림축/탄성영역에서의 응력/탄성비틀림/극관성모멘트 (0) | 2019.05.13 |
'재료역학' Related Articles
more
