상태도 분석 1) gibbs에너지와 상평형도 G-P도 G-T도 G-P-T도 본문
G-P-T 그래프
gibbs에너지 G는 온도(T), 압력(P), 조성(\(n_i\))의 함수입니다.
따라서 G(T,P,\(n_i\))인데, 단성분계에서 조성은 일정한 값이 됩니다. (단성분 (조성은 100프로))
G(T,P)는 T-P-G좌표계에서 에너지면을 나타냅니다.
이는 그림으로,
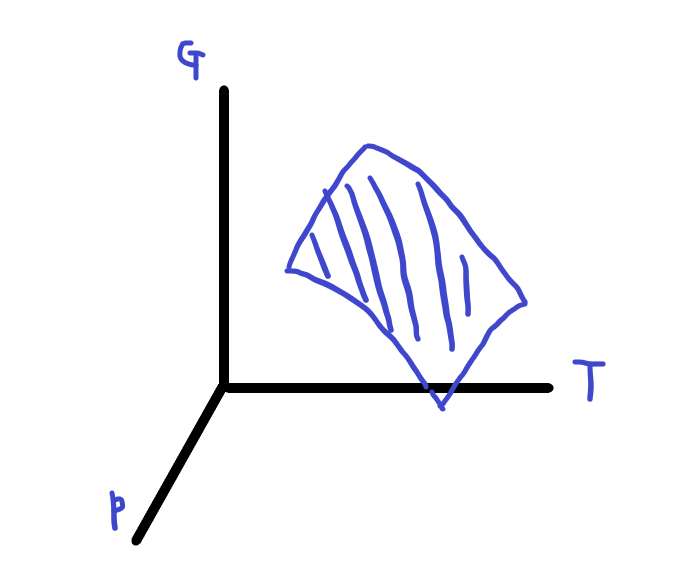
이러한 형태로 나타납니다.
만약 두 계 \(\alpha\),\(\beta\)가 있다고 한다면,
이 두 계의 깁스 에너지는 그림으로
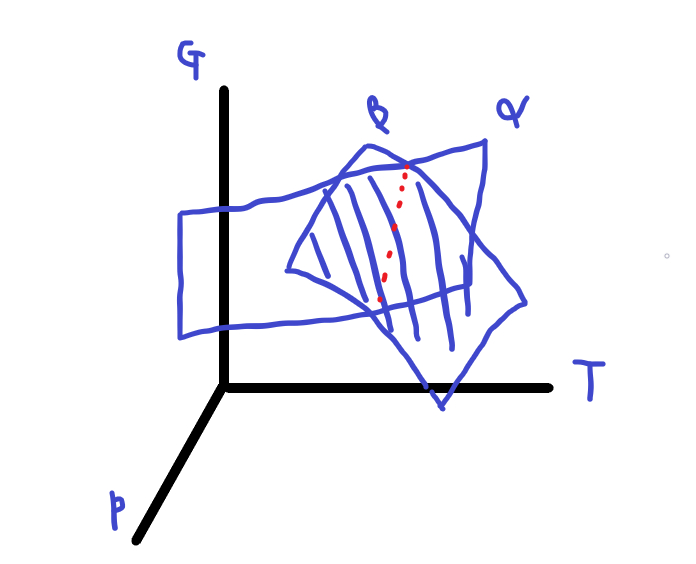
이렇게 나타나게 됩니다.
위의 그림에서 빨간 점선 부분이
계가 평형상태인 부분인데,
두 계가 평형 상태라면 두 계의 깁스 에너지는 같아집니다.
\(G^{\alpha}\)=\(G^{\beta}\)
이때 평형 상태인 경계선 기준 좌측은 \(\alpha\)계의 깁스 에너지가 낮고 우측은 \(\beta\)계의 깁스에너지가
낮음을 볼 수 있습니다. 깁스에너지가 낮으면 더욱 안정되므로, 두 상중 어떤 상이 안정된지 파악할 수 있습니다.
깁스 자유에너지는 단성분계에서 (조성 일정)
dG = VdP-SdT입니다.
또한 깁스에너지를 (T,P에 대한 함수이므로)
dG = \(\frac{\partial G}{\partial P}_T\)dP + \(\frac{\partial G}{\partial T}_P\)dT 로 표현할 수 있습니다.
따라서 V = \(\frac{\partial G}{\partial P}_T\) S = -\(\frac{\partial G}{\partial T}_P\)가
됩니다.
이는 G-T 그래프에서 기울기가 -S
G-P 그래프에서 기울기가 V임을 보여줍니다.
통상적으로 물질의 엔트로피는 양이므로, G=T그래프에서의 기울기는 음수가 되고,
G는 T가 증가함에 따라 감소하게 됩니다.
또한 G-T그래프를 그려보면,
G-T 그래프

의 형태인데, 이때 기울기인 엔트로피가 기체>액체>고체 순이므로
다음과 같이 그려지고,
깁스에너지는 낮을수록 안정되므로,
온도가 낮을때 고상, 높아짐에 따라 액상, 기상 순으로 변함을 알 수 있습니다.
또 깁스 에너지의 곡률은
\(\frac{\partial^2 G}{\partial T^2}_p\) = -\(\frac{C_p}{T}\) 이 됩니다.
곡면은 온도에 대하여 위로 볼록한 형태를 취하는데, 기상,액생,고상의 열용량은 비슷하므로 곡면의 곡률은 비슷한
양상이 됩니다.
G-P 그래프
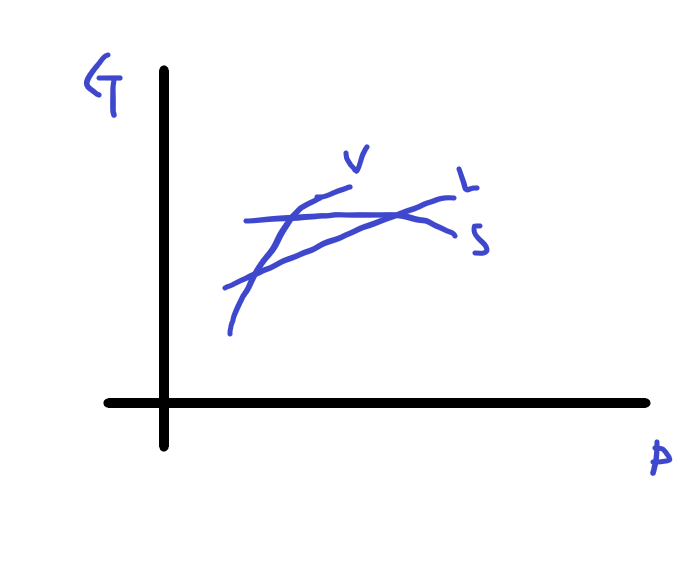
G-P 그래프에서 기울기는 V이고 V는 양이므로 양의 기울기입니다.
즉, Gibbs에너지는 압력이 증가함에 따라 증가합니다.
일반적으로 부피는 고체<액체<기체 순이므로, 그래프는 다음과 같이 그려집니다.
이를 이용해서 단성분계의 상평형도를 그릴 수 있게 되는데,
예를들어 G-P도를 여러 온도에 대하여 구하고
그 온도에 대하여 P-T도를 모식적으로 그리는 것입니다.
'상평형도 분석' 카테고리의 다른 글
| 상태도 분석 5) 중간화합물이란? (0) | 2019.10.16 |
|---|---|
| 상태도 분석 5) 공정반응의 심화 (2) - 공정조성 재료조직 - 침상/층상/골격상/단괴상, 등조성분석, 비평형응고 , 이산공정 (1) | 2019.10.15 |
| 상태도 분석 4) 공정반응의 심화 (1) - 기하요소 (단조성상, 부분고용체, 퇴행고상선) 및 냉각곡선 , 아공정 과공정 , 용해도 (0) | 2019.10.15 |
| 상태도 분석 3) 공정반응이란 정확히 무엇인가? eutectic (1) | 2019.10.15 |
| 상태도 분석 2) 이성분계 응축상률 / 열역학 (화학퍼텐셜) / 응고유형 -단조성상 고용체 중간화합물 (0) | 2019.10.15 |



